Revisión: 1
Fecha: 19 Oct 1997

La página de efectos DSP

Delay, eco, reverberancia

Si se toman el tiempo de leer las consideraciones generales aclararemos algunas asunciones.
La implementación de un delay con DSP no difiere demasiado de la implementación digital; en realidad, lo que hacemos es transferir al software las tareas que realizaba el hardware dentro del bloque de memoria.
Asignaremos un area de memoria como buffer circular, almacenaremos el dato de entrada en una posición indicada por un puntero, y leeremos el dato de salida en otra posición indicada por otro puntero. La diferencia entre ambos punteros, y por ende la cantidad de palabras de memoria, representa el tiempo de delay en períodos de clock. Así, para lograr una demora de 500ms. a una frecuencia de muestreo de 20KHz, serán necesarias 10Kmuestras, por lo que puede usarse un buffer de 16Kwords, y la diferencia entre los punteros será de 10K.
La realimentación y los niveles de señal serán ahora manejados por software, por lo que el dato leído será convenientemente multiplicado por una constante (feedback level) y sumado a la señal original de entrada, por lo que es necesario realizar la escritura en memoria después de la lectura. Ambos datos, el leído de memoria y el tomado de la señal de entrada serán además multiplicados por sendas constantes (direct y effect level) antes de ser sumados y enviados al conversor de salida. Estas multiplicaciones suelen acarrear inconvenientes cuando se trabaja con CPUs que no soportan coma flotante.
Ambos punteros, de lectura y de escritura, serán incrementados a cada intervalo de muestreo, recorriendo circularmente el buffer.
Como la operación de lectura se realiza antes que la de escritura, leer y escribir en la misma posición corresponde al mayor delay posible, mientras que leer en la posición inmediatamente anterior corresponde al menor delay posible, leer la muestra que fue escrita recién en el intervalo pasado. Entonces, en el ejemplo anterior, el puntero de lectura estará 10K words por debajo del de escritura, o, lo que es lo mismo, 16K-10K=6Kwords por encima.

La reverberancia necesita un enfoque totalmente distinto, basado en el estudio de Schroeder y Moorer. Cuando tenga información clara al respecto la pondré disponible.

Flanger, Chorus

Lo hacemos implementando el bloque básico de delay, pero la historia se complica un poco. La modulación del tiempo de retardo no puede hacerse mediante un VCO como en la implementación digital, debe hacerse por software. Esto nos lleva a generar retardos de tiempo que se encuentran en "fracciones de período de reloj", por lo que deberemos realizar una interpolación entre dos muestras para lograr el verdadero valor.
El retardo mínimo es el tiempo de delay especificado (en milisegundos). El retardo máximo es el retardo mínimo más el ancho de modulación (en milisegundos). Se los traduce a muestras de la siguiente forma:
min_delay = delay * fs / 1000
max_delay = ( delay + width ) * fs / 1000, donde fs es la frecuencia de muestreo.
Una vez determinados el retardo mínimo y el retardo máximo, calculados a partir del ancho de modulación (width) y el tiempo de demora, se barre el puntero de lectura en ese intervalo, incrementándolo o decrementándolo acorde lo indica la velocidad de barrido (speed) dentro de ese rango.
La velocidad de modulación del retardo se especifica en ciclos por segundo (Hz), por lo que debe convertirse al incremento a hacerse al puntero.
Deberemos recorrer el número de muestras especificado y regresar, la cantidad especificada de veces en un segundo, y tenemos SAMPLE_RATE intervalos para hacerlo.
Entonces , si se barre con una rampa, el incremento del puntero se calcula como:
step = 2 * width * fm / fs, donde fs es la frecuencia de muestreo, fm es la de barrido, y width es el ancho de barrido calculado en muestras (max_delay - min_delay). Esta cantidad será sumada al incremento normal del puntero de lectura a cada intervalo.
Y, si usamos la función exponencial, se calcula como:
step = (max_delay/min_delay) ^(2fm/fs). Este coeficiente será el valor por el cual se multiplicará el puntero de lectura a cada intervalo.
Si el puntero apunta a la posición 1000,523; deberemos interpolar entre la muestra 1000 y la 1001 para hallar el valor que correspondería a la señal analógica de haber sido muestreada en el instante correspondiente a la muestra 1000,523. El método de interpolación dependerá de la potencia de CPU disponible, y la calidad de efecto deseada. Para fines no profesionales, contrariamente a lo indicado por la teoría, se puede utilizar interpolación lineal, especialmente si la tasa de muestreo es muy superior a la máxima componente de la señal analógica.
La interpolación lineal se realiza facilmente descomponiendo al puntero de lectura en su parte entera y su parte fraccionaria, utilizando la parte entera para leer dos datos contiguos de memoria y la parte fraccionaria para pesar ambos, por ejemplo, [1000,523]=0,523*[1001] + (1-0,523)*[1000], donde [posición] indica el dato almacenado en esa posición, es decir: "Para obtener el dato correspondiente a la posición 1000,523; lo calculamos multiplicando la parte fraccionaria por el contenido de la posición que le sigue, más el complemento a uno de la parte fraccionaria por el contenido de la parte entera de la posición".
O, con una multiplicación menos pero un idexado más, lo mismo puede calcularse como [1000.523]=[1000] + ([1001]-[1000]) * 0.523, lo que es lo mismo que decir : "Para obtener el dato correspondiente a la posición 1000,523; lo calculamos multiplicando la parte fraccionaria por la diferencia entre los contenidos de la parte entera de la posición y la siguiente, más el contenido de la parte entera de la posición".
En el caso del chorus, eliminaremos la realimentación (feedback). Puede usarse el mismo algoritmo y colocar la variable 'feedback' en cero, al costo de un par de ciclos de CPU.
La señal de barrido puede ser una senoide, implementada mediante búsqueda en tabla (table lookup), o mejor aún, la señal exponencial, que produce el mejor chorus que he oído.

Pitch shift

Lo implementamos de forma análoga al chorus, realizando un barrido lineal y reiniciándolo al llegar al límite (sin volver atrás). Para minimizar el salto de fase en el reinicio del barrido, se suele utilizar un segundo puntero en cuadratura con el principal, y fundir los datos leídos por ambos mediante algún método de interpolación.
Como se dijera anteriormente, la pendiente de barrido da la cantidad de desplazamiento, y se la calcula como se indicó.
Otra posibilidad es determinar el período entre cruces por cero de la señal (autocorrelación, simple inspección del buffer), y realizar el barrido entre cruces por cero, de forma tal de evitar el salto abrupto de fase.
Hasta ahora no he implementado con demasiado éxito ninguno de estos sistemas. Siendo el más sencillo el primero, no logro un efecto demasiado agradable con algunas señales.

Compresor/limitador, downward expander, noise gate

Aún no he probado este sistema, por consiguiente lo que sigue a continuación es un planteo teórico basado en otro planteo teórico.
Si se toman el tiempo de leer las consideraciones generales aclararemos algunas asunciones.
Trataremos de implementar los bloques básicos mediante DSP. Tomaremos la señal de entrada y hallaremos su valor medio/eficaz/pico; según deseemos sea la respuesta del compresor. Un limitador tal vez deba responder al valor de pico, a fin de que la señal no sobrepase determinado valor. Un compresor para efecto de sustain tal vez deba responder al valor medio/eficaz, para no achatar demasiado los picos de ataque de la fuente de sonido (una guitarra, por ejemplo). Para hallar estos valores, definiremos algún período de integración durante el cual extraeremos el valor deseado. Cabe destacar que necesitamos que el sistema responda a algún valor de la señal pesado durante un intervalo de tiempo (de ataque); una vez superado el umbral, se considerará que la señal regresó al estado inferior al umbral una vez superado el tiempo de liberación (release). Si actuáramos muestra a muestra, actuaríamos sobre la forma de la señal y no sobre su amplitud.
Trataremos de hallar el valor de la reducción de la ganancia para un compresor/limitador:
El valor de nivel de señal obtenido será comparado contra el nivel de umbral. Como este nivel se especifica en dB (dBm, dBV, dBu, VU, etc.), para evitar hacer la conversión muestra por muestra, resulta conveniente realizar la conversión del nivel de umbral de dB a lineal y comparar muestra por muestra con este valor. Sabiendo que la reducción de la ganancia es Vi[dB]-Vo[dB], reemplazamos Vo[dB] por la ecuación del compresor/limitador, resultando GR = (Vi[dB]-Vt[dB]) * (1 - 1 / CR)
Si no se supera el valor de umbral, simplemente no hacemos nada, dejamos pasar la señal tal cual es. Si se supera el valor, calculamos la ecuación anterior convirtiendo Vi a dB mediante búsqueda en tabla (table lookup), restándole el valor Vt en dB (ya conocido), y multiplicando por uno menos la recíproca de la relación de compresión. El resultado obtenido es la reducción de la ganancia (atenuación) en dB necesaria, deberemos pasar este valor a lineal y hallar su recíproca, lo que nos dará el coeficiente de ganancia. En el ejemplo de la definición de compresor, 1 - 1 / CR resulta 1 - 1/4 = 0,75, y (30 - (-10)) * 0,75 = 30
En el caso del limitador (compresión infinita), el término uno menos la recíproca de la relación de compresión resulta igual a uno, por lo que directamente atenuamos la señal en dB la misma cantidad en que ésta excede al umbral; lo que resulta coherente.
Almacenaremos este coeficiente obtenido, ya que será la ganancia por la cual multiplicaremos muestra a muestra la señal de entrada hasta que en el próximo período de integración resulte otro valor y ésta se modifique.
Para el caso del downward expander, realizaremos la misma operación pero a la inversa: superar el umbral será tener una señal de valor inferior al umbral, y la relación de expansión ya es la inversa de la relación de compresión; por lo que uno menos la recíproca de la relación de compresión resulta uno menos la relación de expansión, que será negativo, indicando que la reducción de la ganancia es en realidad un aumento de la ganancia; lo que coincide con lo expresado en la teoría.
Para el caso del noise gate (un downward expander con expansión infinita), nos limitaremos a dejar pasar la señal sólo cuando se supera el umbral.
El tiempo de release se implementa fácilmente de forma analógica, dejando que un capacitor cargado a la tensión de control del atenuador simplemente se descargue, controlando la liberación en forma exponencial decreciente, y por ende linealmente en dB. En DSP, deberemos hallar otro coeficiente que nos permita llegar, al cabo de N multiplicaciones sucesivas a lograr que el coeficiente de ganancia se reduzca en 20 dB (esto sería nuestro equivalente a la aproximación de la constante RC). Este coeficiente se determina de forma similar al coeficiente de la función exponencial usada para barrer el retardo en chorus y phasers.
release = 10 ^ (1/fs), donde fs es la frecuencia de muestreo.
Queda como tarea para los más delirantes la aproximación de la constante RC mediante la transformación bilineal, de manera similar al desarrollo del phaser DSP.

Phaser o phase shifter

Si se toman el tiempo de leer las consideraciones generales aclararemos algunas asunciones.
Para lograr un phaser con DSP se puede recurrir a implementar la ecuación diferencia de un filtro all-pass. Sin embargo, puede resultar más interesante reproducir fielmente el sonido del phaser analógico original. Para esto, tomamos la ecuación de transferencia de una red desfasadora analógica en el plano s y la pasamos al plano z mediante la transformación bilineal. Luego, implementamos la ecuación diferencia resultante, en la cual el coeficiente determinado guardará una estrecha relación con la red RC original y el período (Td) entre muestras.



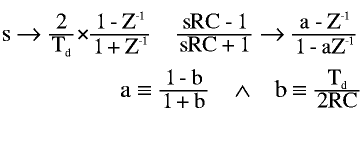
La ecuación diferencia resultante es:

y[n] = a ( x[n] + y[n-1] ) - x[n-1]

Un phaser se define por la frecuencia base (aquella a la cual wRC=1 para R máxima) y la frecuencia máxima (aquella a la cual wRC=1 para R mínima) o su rango en octavas; controlado por la perilla de ancho de modulación (width).



La señal utilizada para barrer deberá ser una función de tipo exponencial, ya que no tenemos detalles constructivos que compensar:
step = (b_max/b_min) ^(2fm/fs), donde fm es la frecuencia de barrido y fs es la frecuencia de muestreo. Este coeficiente será el valor por el cual se multiplicará al coeficiente b a cada intervalo.
El efecto logrado es superior al viejo phaser analógico original (Q.E.P.D.).

Consideraciones generales

Aclaraciones adicionales

Buffer circular

Un buffer circular en software es similar al de hardware, excepto que el 'wrap-around' del puntero debe hacerse por soft, a menos que la CPU provea soporte para buffers circulares por hardware, como el ADSP2181 de Analog Devices. Este 'wrap-around' consiste en volver al inicio del buffer cuando se supera el final del mismo, y suele realizarse fácilmente utilizando un índice dentro del buffer (que va desde 0 hasta la longitud del buffer menos uno) y realizando el AND del índice con la longitud del buffer menos uno (un buffer de 1K implica AND con 0x3FF) en cada operación con el índice.
Así, un retardo de 500 ms a una frecuencia de muestreo de 20KHz necesita 10Ksamples, por lo que en un buffer de 16K (0x4000) haremos un AND con 0x3FFF.

Enteros vs. coma flotante

El problema de usar una CPU que no maneja números en formato de coma flotante es bien conocido por todos quienes transitan por los caminos del DSP; sin embargo, nunca está de más repasar algunos detalles. En estos efectos realizamos algunas multiplicaciones y sumas, pudiendo llegar a 'desbordar' el ancho de palabra de trabajo. Es fundamental restringir el desborde a una saturación (ej.: 240+30=255 en 8 bits) a fin de simular lo que ocurriría en un sistema analógico. Caso contrario, si dejáramos que el desborde normal ocurriera (ej.: 240+30=14 en 8 bits), estaríamos produciendo cosas sumamente extrañas y desagradables sobre la señal. Las nuevas CPU dedicadas a DSP incorporan un modo especial de overflow para estos fines.
Se realizan muchas operaciones con números fraccionarios, por lo que si nuestra CPU soporta sólo enteros, deberemos simularlos usando algún formato de coma fija como por ejemplo 1.15 (1 bit de entero/signo y 15 de fracción).
Esto complica un poco la aritmética, a menos que la CPU soporte números fraccionarios con coma fija (como la mayoría de los DSP).

Transformación bilineal

En la transformación bilineal, se reemplaza la variable s por una función de la variable z, resultando un mapeo de los polos y ceros del plano complejo s en el plano complejo z. En particular, el eje jw resulta mapeado en la circunferencia unitaria, por lo que todos los polos o ceros que se hallen en el eje jw resultarán en la circunferencia de radio uno, y todos los polos o ceros que se hallen a la izquierda del eje jw resultarán dentro de la circunferencia de radio unitario. Así, los criterios de estabilidad de uno y otro mundo resultan comunes, y las respuestas de ambos sistemas resultan equivalentes.

Función exponencial

Esta función recorre distancias iguales (en octavas) en tiempos iguales. Lo hace moviéndose de forma exponencial, de modo de ser una rampa en un eje logarítmico. Como un movimiento en octavas supone multiplicar por 2 cada vez, la ecuación del movimiento es y = y0 * 2 ^x, y0 es la posición inicial, y 2 es el incremento deseado. Calcularemos ahora la ecuación de esta función basándonos en la aplicación de técnicas de DSP.
Tenemos dos límites, uno inferior y0 y uno superior y1; debemos recorrer el camino y regresar (un ciclo) en un segundo (1Hz), lo que significa que tenemos SAMPLE_RATE intervalos para hacerlo. Si con cada intervalo multiplicamos a y0 por un coeficiente a, tal que al cabo de SAMPLE_RATE/2 intervalos lleguemos a y1, resulta a = (y1/y0) ^(2/fs), donde fs es la frecuencia de muestreo (el número de muestras por segundo).
Si queremos realizar más ciclos por segundo, debemos hacer que a se haga más grande, para que con menor número de multiplicaciones recorramos la misma distancia, por lo que resulta a = (y1/y0) ^(2fm/fs), donde fm es la frecuencia de barrido en Hz.
Por ende, la función deseada será y = y0 * a ^n, donde n es la variable independiente y representa el número de muestra.
Si miramos esta función en una escala logarítmica, resulta ln y = n * ln(a * y0) , siendo a e yo constantes, es decir, es una recta. Como vemos , esta función recorre espacios iguales (en octavas) en tiempos iguales.
La derivada de esta función será y' = y0 * a ^n * ln a, lo que equivale a la misma función cambiada de escala por el término ln a, que es constante; con lo cual también recorrerá espacios iguales (en octavas) en tiempos iguales.
Al retroceder desde y1 hasta y0, usaremos el mismo camino, dividiendo por a en vez de multiplicar, o lo que es lo mismo, hacemos a = 1/a, por lo que todo lo anterior resulta igualmente válido, ya que recorrer 2 octavas hacia arriba equivale a multiplicar por 4, y recorrer dos octavas hacia abajo equivale a dividir por 4 o multiplicar por 1/4.
Esta función es muy difícil de implementar en forma analógica, por lo que su utilización queda practicamente limitada a sistemas DSP.

This page hosted by Get your own Free Home Page