Revision: 1
Date: Oct 19^rd, 1997

The DSP effects page

Delay, echo, reverberation

If you take the time to read the general considerations we'll clarify some points first.
The implementation of a DSP delay does not differ too much from the digital implementation; in fact, what we do is to transfer to software the tasks previously done by hardware inside the memory block.
We'll designate a memory area as a circular buffer, where we will store the input data at a location pointed to by a pointer, and will read from another location, pointed to by another pointer. The difference between both pointers, and so the number of memory words between them, represents the delay time in clock periods. So, to get a 500ms delay time at a 20KHz sampling frequency, a 10Ksample space will be needed, so the buffer could be a 16Kwords buffer, and the pointers difference will be 10K.
Feedback and signal levels will now be handled by software, so the read data will be conveniently multiplied by a constant (feedback level) and added to the original input signal, so memory writing must be performed after memory reading. Both data values, the one read from memory and the one taken from the input, will be multiplied by different constants (effect level and direct level respectively), before being added and the value sent to the output converter. This multiplications and additions are fond of causing problems when working with integer CPUs.
Both, read and write pointers, will be incremented at each sampling interval, wrapping around the buffer.
As the read operation is performed before the write operation, reading and writing at the same location corresponds to the larger delay, and reading at the location just below corresponds to the smaller delay, reading a sample that was just written the last interval. In the former example, the read pointer will be pointing 10K words below the write pointer, or 16K-10K= 6Kwords above.

Reverberation needs a totally different approach, based on works from Scroeder and Moorer. As soon as I have some clear info on this subject, I'll publish it here.

Flanger, Chorus

This is implemented building the delay basic block, but things get now a bit complicated. The time delay modulation can't be done by a VCO as in the digital implementation, it must be done in software. This leads us to generate time delays in "fractions of clock period", so an interpolation between two samples is needed to get the real value.
The minimum delay is the delay time (in milliseconds) specified. The maximum delay is the minimum delay plus the modulation width time (in milliseconds). They are translated to samples as follows:
min_delay = delay * fs / 1000
max_delay = ( delay + width ) * fs / 1000, where fs is the sampling frequency.
Once the minimum and maximum delays are determined, calculated from the modulation width and delay time data, the read pointer is swept inside that interval, being incremented or decremented as the sweep speed indicates.
The time delay modulation speed is specified in cycles per second (Hz), so a conversion to the needed pointer increment should be performed.
We have to travel the specified number of samples and return back the number of times specified, and we have SAMPLE_RATE time intervals to do it in a second.
So, if a linear ramp is used, the pointer increment will be calculated as follows:
step = 2 * width * fm / fs, where fs is the sampling frequency, fm is the sweep frequency, and width is the calculated sweep width in samples (max_delay - min_delay). This amount will be added to the normal read pointer increment at every interval.
And, if the exponential function is used, the pointer increment will be:
step = (max_sweep/min_sweep) ^(2fm/fs). This coefficient is the value which the read pointer will be multiplied by at every interval.
If the pointer points to location 1000.523; we´ll have to interpolate between sample 1000 and sample 1001 to get the value corresponding to the analog signal if it were sampled at the time instant corresponding to sample 1000.523. The interpolation method used will depend on CPU power available and the desired effect quality. For non-professional purposes, against theoretical aseverations, linear interpolation can be used, particularly if the sampling rate is quite higher than the analog signal´s highest frequency component.
Linear interpolation is easily done by decomposing the pointer in an integer and a fractional part, using the integer part to read two contiguous memory locations and the fractional part to weight both values, for example, [1000.523]=0.523*[1001] + (1-0.523)*[1000], where [location] means the data value stored at that location, that is: "To get the data value corresponding to location 1000.523; we calculate it by multiplying the fractional part by the content of the next location plus the fractional part´s one complement multiplied by the content of the integer location".
Or, with one less multiplication but an additional indexing operation, the same stuff can be calculated as [1000.523]=[1000] + ([1001]-[1000]) * 0.523, what is saying: "To get the data value corresponding to location 1000.523; we calculate it by multiplying the fractional part by the difference between the contents of the integer location and the next location, plus the contents of the integer location".
In the case of chorus, we'll eliminate the feedback. The same algorithm can be used, by setting the 'feedback' variable to cero, at the expense of a couple of CPU cycles.
The sweep signal for a chorus could be a sine, implemented by a table lookup, or, yet better, the exponential signal, which produces the best chorus sound I've ever heard.

Pitch shift

This is implemented as a chorus, sweeping through the defined delay width and restarting once the limits are reached (no sweep back). To minimize the phase jump at the sweep restart, a second pointer is often used, in quadrature with the former, and both pointer´s data are cross-faded together with some interpolation method.
As it has been told before, the sweep slope gives the pitch shift amount, and so it is calculated as it was explained.
Another possibility is to determine the signal zero crossing period (autocorrelation, buffer inspection), and perform the sweep between zero crossings, in order to avoid the abrupt phase jump.
Up to now, I haven't succesfully built none of these systems. Being the first one the easiest, I can't get a pleasing effect with some signals.

Compressors/limiters, downward expanders and noise-gates.

I haven't tried this system yet, so what follows is a theoretical development based on another theoretical development.
If you take the time to read the general considerations we'll clarify some points first.
We'll try to implement the basic building blocks with DSP. We'll take the input signal and find its mean/RMS/peak value; depending on the compressor response needed. A limiter might probably respond to a peak value, in order for the signal to exceed certain value. A sustain effect compressor might need to respond to mean/RMS value, not to make too flat the normal attack peaks the signal has (a guitar for example). To find these values, we'll set an integration period, during which we'll extract the needed value. It is important to notice that we need the system to act upon a signal value weighted on a time interval (attack time); after this threshold is exceeded, we'll consider that the signal is back on the other side (lower than the threshold) once another period is elapsed (release time). Should we act on a sample by sample basis, we'll end up transforming the signal's shape instead of its amplitude.
Let's try to find a compressor/limiter's gain-reduction:
The signal value obtained will be compared to the threshold level. As this level is specified in dB (dBm, dBV, dBu, VU, etc.), to avoid converting on each sample interval, it is convenient to convert this threshold level fron dB to linear, and compare sample by sample with this value.
Knowing that gain-reduction is Vi[dB]-Vo[dB], let's replace Vo[dB] with the compressor/limiter's equation, resulting GR = (Vi[dB]-Vt[dB]) * (1 - 1 / CR)
If the threshold level is not exceded, we simply do nothing, we let the signal pass through as it is. If the threshold level is exceded, we calculate the former equation converting Vi to dB by a table lookup, substracting the already known Vt in dB, and then multiplying by one minus the compression ratio's reciprocal. The obtained result is the gain-reduction (attenuation) in dB needed, we'll convert this value to linear and find its reciprocal, which will give us the gain coefficient. In the definition example, 1 - 1 / CR is 1 - 1/4 = 0.75; and (30 - (-10)) * 0,75 = 30
On the limiter (infinite compression), the term one minus the compression ratio's reciprocal is equal to unity, so the signal is attenuated in dB the same amount it excedes the threshold level; what sounds coherent.
We'll store this obtained coefficient value, as it will be the gain by which we'll multiply sample by sample the input signal, until in the next integration period a different value results and the gain is altered.
For the downward expander, we'll perform the same operation, but in a reverse way: to exceed the threshold now means having a signal whose value is less than the threshold level, and the expansion ratio is already the reciprocal of the expansion ratio; so one minus the compression ratio's reciprocal is now one minus the expansion ratio, what is negative, indicating that gain-reduction is now gain increase instead.
For the noise gate (an infinite expansion downward expander), we'll let the signal pass through when it excedes the threshold level.
The release time is easily implemented with analog techniques, letting a capacitor charged to the attenuator control voltage to simply discharge, controlling the release in a decreasing exponential way, and so linearly in dB. With DSP, we'll have to find another coefficient that lets us reach, after N succesive multiplications, the gain coefficient reduction in 20 dB (this would be our equivalence to the RC time constant approximation). This coefficient is determined in a similar way as the exponential function used to sweep the delay in chorus and phasers.
release = 10 ^ (1/fs), where fs is the sampling frecuency.
It is left to the most weird readers the RC constant approximation by means of a bilinear transform, similar to the phaser in DSP.

Phaser or phase shifter

If you take the time to read the general considerations we'll clarify some points first.
To make a phaser out of a DSP, one can implement an all-pass filter difference equation. Nevertheless, reproducing the analog phaser's original sound can be more interesting. So, we take a phase shifter network's transfer function on the s plane and pass it to the z plane, by means of a bilinear transform. Then, the resulting difference equation is implemented, and the resulting coefficient will depend on the original RC network and the sampling period Td.



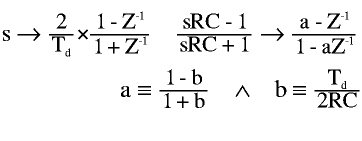
The resulting difference equation is:

y[n] = a ( x[n] + y[n-1] ) - x[n-1]

A phase shifter effect is defined by its base frequency (the one at which wRC=1 for maximum R) and its top frequency (wRC=1 for minimum R) or the range in octaves; which is controlled as the width knob.



The sweeping function must be an exponential function, 'cause there are no constructive aspects to compensate:
step = (b_max/b_min) ^(2fm/fs), where fm is the sweep frequency and fs is the sampling frequency. This coefficient is the value which the b coefficient will be multiplied by at every interval.
The effect so obtained is quite superior to the original analog phaser (R.I.P.).

General considerations

Additional explanations

Circular buffer

A software circular buffer is similar to a hardware one, except that the pointer 'wrap-around' must be done in software, unless the used CPU supports hardware circular buffers, as the ADSP2181 from Analog Devices. This wrap-around consists of returning to the buffer head when the tail is reached or exceded, and is often done by using an index into the buffer (which runs from 0 to buffer lenght minus one) and ANDing it with the buffer lenght minus one (a 1K buffer means ANDing the index with 0x3FF) upon every index operation.
This way, a 500 ms delay at a 20 KHz sampling frequency needs 10Ksamples, so in a 16K (0x4000) buffer we'll AND with 0x3FFF.

Integer vs. Floating point

The problem of using an integer CPU is well known to everybody working in DSP; nevertheless, it is not a waste of time to point out some details.
In these effects, we perform many multiplications and additions, getting to overflow the word lenght. It is fundamental to restrict this overflow to a saturation (e.g.: 240+30=255 in 8 bits), in order to simulate what would occur in an analog system. Otherwise, if we should let the standard overflow to occur (e.g.: 240+30=14 in 8 bits), we´ll be introducing strange and unpleasing artifacts to the signal. The new DSP oriented CPUs have a built in special overflow handling mode for this task.
A lot of operations with fractional numbers is done, so if our CPU is an integer one, we'll have to emulate fractional numbers by using a fixed point notation as 1.15 (1 sign/integer bit, 15 fraction bits). This complicates the arithmetic, so a CPU handling fixed point fractional numbers (as all the DSP chips) is preferred, and a floating point CPU is best (although more expensive)

Bilinear Transform

In bilinear transformation, the s variable is replaced by a function of the z variable, resulting in a mapping of the poles and zeros of the s complex plane in the z complex plane. In particular, the jw axis is mapped to the unit circle, so every pole or zero on the jw axis is mapped to the unit circle, and all the poles or zeros at the left of the jw axis will be mapped inside the unit circle. So, stability criteria from both worlds will be common, and both system's responses will be equivalent.

Exponential function

This function travels equal distances (in octaves) in equal times. It does so by moving in an exponential way, so it is a ramp in a logarithmic axis. As a movement in octaves is multiplying by 2 each time, the movement equation is y = y0 * 2 ^x, y0 is the initial position, and 2 is the desired increment. We'll now calculate this function equation based on the application of DSP techniques.
Let's have two bounds, a lower bound y0 and an upper bound y1; we have to move from the lower bound to the upper one and come back (one cycle) in a second (1Hz), this means we have SAMPLE_RATE time intervals to do it. If at every time interval we multiply y0 by a certain coefficient a, which makes that after SAMPLE_RATE/2 times we reach y1; then a = (y1/y0) ^(2/fs), where fs is the sampling frequency (the number of samples per second).
If we want to do more cycles per second, we´ll have to make a bigger, in order to travel the same distance with less multiplications, so now a = (y1/y0) ^(2fm/fs), where fm is the sweep frequency in Hz.
Then, the desired function will be y = y0 * a ^n, where n is the independent variable and represents the sample number.
If we look at this function on a logarithmic scale, we see ln y = n * ln(a * y0) , being a and yo constants, this is a straight line. As we see, this function travels equal spaces (in octaves) in equal times.
This function´s derivative will be y' = y0 * a ^n * ln a, and this is the same function changed in scale by the term ln a, which is a constant; so it will also travel equal spaces (in octaves) in equal times.
Going back from y1 to y0, we'll use the same path, dividing by a instead of multiplying, or , same thing, make a = 1/a, so the former analysis ends up being also valid. Going 4 octaves up means multiplying by 4, and going 4 octaves downwards means dividing by 4 or multiplying by 1/4. A function like this is quite difficult to implement by analog techniques, so its use is practically limited to DSP systems.

This page hosted by Get your own Free Home Page